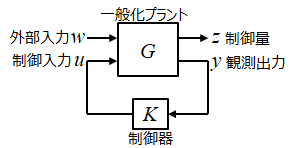
移植したコード「プログラム4.5」
import numpy as np
import matplotlib.pyplot as plt
import control
from control.matlab import *
m1 = 0.8;
m2 = 0.2;
k1 = 100;
c1 = 1;
c2 = 0.3;
Ks = 100;
M = np.matrix([ [ m1, 0 ],
[ 0, m2 ] ]);
C = np.matrix([ [ c1+c2, -c2 ],
[ -c2, c2 ] ]);
F = np.matrix([ [ Ks ],
[ 0 ] ]);
iM = np.linalg.inv(M);
Bp = np.concatenate([ np.zeros((2,1)), iM*F ]);
Cp = [ 0, 1, 0, 0 ];
Dp = 0;
w = logspace(0,3,100);
k2 = 300;
K_ = np.matrix([ [ k1+k2, -k2 ],
[ -k2, k2 ] ]);
Ap = np.concatenate([
np.concatenate([np.zeros((2,2)), np.eye(2)], axis=1),
np.concatenate([ -iM*K_, -iM*C ], axis=1) ]);
P_nominal = ss( Ap, Bp, Cp, Dp );
Pn = ss2tf(P_nominal);
s = tf('s');
Wm = 3*s**2/(s**2+18*s+45**2);
Ws = 15/(s + 1.5e-2);
Wps = Ws*0.8;
Wt = Wm;
Weps = 5e-4;
plt.figure(3)
mag,phase,om = bode(Ws, w, plot=False);
plt.semilogx(om, 20*np.log10(mag), ':', label='$W_S$');
mag,phase,om = bode(Wps, w, plot=False);
plt.semilogx(om, 20*np.log10(mag), label='$W_{PS}$');
mag,phase,om = bode(Wps*P_nominal, w, plot=False);
plt.semilogx(om, 20*np.log10(mag), '-.', label='$W_{PS}*P$');
mag,phase,om = bode(Wt, w, plot=False);
plt.semilogx(om, 20*np.log10(mag), '--', label='$W_T$');
plt.xlim()
plt.ylim(-60, 30);
plt.legend();
WpsP = Wps*Pn;
WpsE = Wps*Weps;
num = [[WpsP.num[0][0], WpsE.num[0][0], (-WpsP).num[0][0]],
[ [0], [0], Wt.num[0][0]],
[ Pn.num[0][0], [Weps], (-Pn).num[0][0]]];
den = [[WpsP.den[0][0], WpsE.den[0][0], (-WpsP).den[0][0]],
[ [1], [1], Wt.den[0][0]],
[ Pn.den[0][0], [1], (-Pn).den[0][0]]];
G_ = tf(num, den)
G = tf2ss(G_)
K, CL, gam, rcond = control.hinfsyn(G,1,1)
print(gam)
plt.figure(4)
mag1, phase1, om1 = bode( P_nominal, plot=False );
plt.semilogx( om1, 20*np.log10(mag1), '--', label='$P_{nominal}$' );
mag2, phase2, om2 = bode( K, plot=False );
plt.semilogx( om2, 20*np.log10(mag2), label='$K$' );
plt.ylim(-60, 60);
plt.xlim(1e0, 1e2);
plt.legend();
L = P_nominal*K;
T = feedback(L,1);
S = feedback(1,L);
plt.figure(5);
mag, phase, om = bode( T, w, plot=False );
plt.semilogx( om, 20*np.log10(mag), '-', label='$T$' );
mag, phase, om = bode( 1/Wt, w, plot=False );
plt.semilogx( om, 20*np.log10(mag), ':', label='$1/W_T$' );
mag, phase, om = bode( S, w, plot=False );
plt.semilogx( om, 20*np.log10(mag), '--', label='$S$' );
mag, phase, om = bode( 1/(Wps*P_nominal), w, plot=False );
plt.semilogx( om, 20*np.log10(mag), '-.', label='$1/(W_{PS}*P)$' );
plt.xlim(1e0, 1e2);
plt.ylim(-30, 30);
plt.legend();
delta = np.arange(-1, 1.01 , 0.1)
for i in range(len(delta)):
k2 = 300+300*0.2*delta[i];
K_ = np.matrix([ [ k1+k2, -k2 ],
[ -k2, k2 ] ]);
Ap = np.concatenate([
np.concatenate([np.zeros((2,2)), np.eye(2)], axis=1),
np.concatenate([ -iM*K_, -iM*C ], axis=1) ]);
P = ss(Ap,Bp,Cp,Dp);
L = P*K;
T = feedback(L,1);
M = feedback(P,K);
yout, time = step( T, 2 );
plt.figure(6);
plt.plot(time, yout);
yout, time = impulse( M, 2 );
plt.figure(7);
plt.plot(time, yout);
(AならばB)が成り立つとき、BはAの必要条件であるという。AであるためにはBである「必要」があるから必要条件。うん、BじゃなかったらAじゃないからBである必要があるよな。わかる。