無料で実践ロバスト制御④ ーH∞制御問題を解くー

平田氏の著書「実践ロバスト制御」↓を無料のPython-Controlで勉強する試み④。

作者:平田光男
コロナ社

Python-ControlでH∞制御問題が解けたので，どのようにしたかを書いておく。
Python-ControlにはH∞制御問題を解く関数(hinfsyn)が用意されているので，MATLABのソースを少し修正して移植するだけで簡単にできると思ったが，案外苦労した。

H∞制御問題の概要

ここで，H∞制御問題の概要を説明しておく。H∞制御では，制御対象Gを下図のような「一般化プラント」の形で表す。

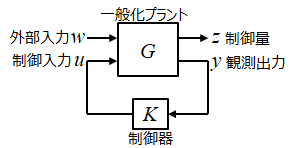
H∞制御の目的は，外部入力wから制御量zまでの伝達関数をなるべく小さくするような制御器Kを求めることである。おそらく，最初にこの一般化を考えた人は，wを指令値，zを偏差などとして，偏差をなるべく小さくするような制御器Kを求めればよい，と考えたのではなかろうか。だが，問題はそんなに単純ではなかった。zは何でも良いわけではなく，「混合感度問題」となるように決める必要がある。
また，この問題は，解析的に式では解けなかった。だが，コンピュータを使えば解けたも同然の結果が得られる。それは，「wからzまでの伝達関数のH∞ノルム(大きさ)がある定数γより小さくなる制御器Kが存在するかどうか」というのを判定でき，存在するならその制御器を求められる方法が発見されているからである。それさえ判定できるのなら，コンピュータでγをいろいろ変えて何度も計算して一番小さいγを探せる(γ-イタレーションという)。この解き方はなかなか数学的に難解であるが，MATLABやPython-Controlなどの関数になっているので詳細を理解しなくても道具としては使えるのである。

H∞制御系設計手順

MATLABやPython-Controlで関数hinfsynを使えば，以下のような手順でH∞制御問題を解ける。
１．制御対象の摂動を定義する
２．乗法的摂動のボードゲイン線図を描く
３．それを覆うように重み $W_T$ を決める
４．感度関数に対する重み $W_S$ を決める
５．一般化プラントGを定義
６．解く！ hinfsyn

重み関数をどのように決めればよいか，などは後日説明することにして，まずは上記の解き方の流れを一通り確認する。
前回↓
無料で実践ロバスト制御③ ー摂動を持つ制御対象ー - manvaのエンジニアリング魂
で上記手順１までできたので，今回はその続きで，手順２から６まで(教科書のプログラム4.2, 4.3, 実行4.1, 4.2)を進めた。

教科書の「プログラム4.2」を移植

手順２．乗法的摂動のボードゲイン線図を描く

プログラム4.2では，まず前回求めた，摂動のある制御対象の摂動部分のみを乗法的摂動の形で取り出し，周波数応答のゲイン線図を描く。(乗法的摂動とは，摂動のある制御対象 $\tilde{P}$ を $\tilde{P}=(1+\Delta_m)P$ の形で表した $\Delta_m$ の部分)。教科書では，不確かさを持つプラントの周波数応答を計算するためにMATLABのufrdというコマンドを使っており，これがPython-Controlにはないが，これは図を描くためだけなので前回までのようにfor文でパラメータを少しずらしながら何回も描けばよい。

手順３．それを覆うように重み $W_T$ を決める

その後，それを覆う(全ての周波数で少し上になる)ように重み関数 $W_m(s)$ を決める。それは教科書ではもう求められている((4.20)式)ので，それをプロットするだけだ。

移植したコード「プログラム4.2」

↓は前回のプログラム実行後に実行する。

#%% 乗法的摂動の見積もり
s = tf('s');
k2 = 300;
K = np.matrix([ [ k1+k2, -k2 ],
                [ -k2,    k2 ] ]);
Ap = np.concatenate([
     np.concatenate([np.zeros((2,2)),  np.eye(2)], axis=1),
     np.concatenate([          -iM*K,     -iM*C ], axis=1) ]);
# %% ノミナル制御対象の定義
P_nominal = ss( Ap, Bp, Cp, Dp );
Pn = ss2tf(P_nominal);

plt.figure(2)
delta_ = np.arange(-1, 1.01 , 0.1)
delta = np.delete(delta_,10)

for i in range(len(delta)):
    k2 = 300+300*0.2*delta[i];
    K = np.matrix([ [ k1+k2, -k2 ],
                    [ -k2,    k2 ] ]);
    Ap = np.concatenate([
         np.concatenate([np.zeros((2,2)),  np.eye(2)], axis=1),
         np.concatenate([          -iM*K,     -iM*C ], axis=1) ]);
    # %% 制御対象の定義
    P = ss(Ap,Bp,Cp,Dp);
    P_g = ss2tf(P);
    Dm_g = (P_g - Pn)/Pn; #% 乗法的摂動の計算
    #%% ゲイン線図のプロット
    #bodemag(Dm_g,'--',Wm,'r-',w)
    mag, phase, om = bode( Dm_g, logspace(0,3), plot=False );
    plt.semilogx( om, 20*np.log10(mag), '--' );

#%% 重み Wm の定義
Wm = 3*s**2/(s**2+18*s+45**2);
mag2, phase2, om2 = bode( Wm, plot=False );
plt.semilogx( om2, 20*np.log10(mag2) );

実行結果

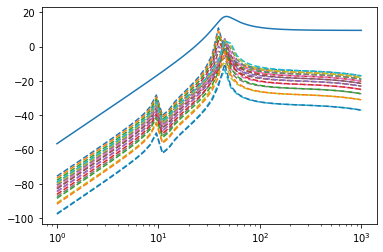
教科書の図4.5と同じ図が描けた。(第2共振付近がちょっと怪しいが)

教科書の「プログラム4.3」を移植

次に，「プログラム4.3」に移る。

手順４．感度関数に対する重み $W_S$ を決める

教科書のこの例では，簡単に(4.22)式のようにほぼ積分のみの関数に決めている。

手順５．一般化プラントGを定義

以下では，一般化プラントを定義する。
教科書(MATLAB)では，一般化プラントをsysicというコマンドで定義しているが，これがPython-Controlにはない。教科書のやり方を確認すると，

G = sysic;

の後は，ここで求めたGをhinfsynに↓

[K,clp,gamma_min,hinf_info] = hinfsyn(G,1,1,'display','on');

のように代入するだけなので，これをPython-Controlに移植するためにはsysicが何を出力しているか理解する必要があった。Python-Controlのhinfsynのドキュメントでは，Gは「partitioned lti plant」としか書かれていないので困った。
MATLABのsysicについては教科書p27に説明があり，一般化プラントの「状態空間実現」を求めているとのこと。つまり，

$\displaystyle{\begin{eqnarray} \dot{x}&=&Ax+B\begin{bmatrix}w\\u\end{bmatrix}\\ \begin{bmatrix}z\\y\end{bmatrix}&=&Cx+D\begin{bmatrix}w\\u\end{bmatrix} \end{eqnarray}}$

という形でGを表す行列A,B,C,Dを求めれば良さそう。
Python-Controlでも同じだろうと考え，これを求めようとしたが，それもなかなか厄介。図4.6より，

$\displaystyle{\begin{eqnarray} z_1&=&W_S(w_1-u)\\ z_2&=&W_Tu\\ y&=&P(w_1-u)+\epsilon w_2 \end{eqnarray}}$

なので，Ws, Wt, Wepsをコマンドssで状態空間モデルにし，

G1 = [ Ws, 0, -Ws ]
G2 = [  0, 0, Wt ]
G3 = [ P, Weps, -P ]
G = [ G1; G2; G3 ]

みたいにつなげれば良いと思ったが，MATLABでは状態空間モデルで上記のような書き方ができる(↓参照)
モデルの結合 - MATLAB & Simulink Example - MathWorks 日本
が，Python-Controlは，series, parallel, feedback, appendは使えるが，[ , ]や[ ; ]に相当するつなぎ方がないっぽい。
結局，状態空間モデルにせず，MIMO(多入力多出力)のtfを使って伝達関数モデルでGを定義し，後から状態空間モデルにしたらできた。MIMOのtfは，3次元の配列(どの入力からどの出力までかが行列のイメージで２次元配列になっており，その各要素が係数のリストなので計３次元)で与える。上記のG1,G2,G3を分子，分母それぞれの係数のリストにした配列を作れば良い。伝達関数モデルで定義したらSISOでも内部的にはnumやdenがリストの２次元配列になっているようなので，「[0][0]」をつけている。

num = [[Ws.num[0][0],    [0], (-Ws).num[0][0]], 
       [         [0],    [0],    Wt.num[0][0]],
       [Pn.num[0][0], [Weps], (-Pn).num[0][0]]]
den = [[Ws.den[0][0],    [1], (-Ws).den[0][0]], 
       [         [1],    [1],    Wt.den[0][0]],
       [Pn.den[0][0],    [1], (-Pn).den[0][0]]]
G_ = tf(num, den)
G = tf2ss(G_)

手順６．解く！ hinfsyn

ここまでできれば後は関数hinfsyn ↓で解くだけだ。
https://python-control.readthedocs.io/en/0.8.3/generated/control.hinfsyn.html
関数hinfsynへの引数は，(P, nmeas, ncon)の３つあり，Pに一般化プラントGを与える。一般化プラントGへの入力は，図↓

のイメージのように， $w$ と $u$ を(縦にこの順で)並べたベクトル，出力は $z$ と $y$ を並べたベクトルなので，Gへの入力ベクトルのうち下からいくつ目までが $u$ で，Gからの出力ベクトルのうち下からいくつ目までが $y$ かを引数nmeas, nconで与えてやればよい。

移植したコード「プログラム4.3」「実行4.1」「実行 4.2」

import control
from control.matlab import *

#%% defgp.m
#%% 重み関数の定義
s = tf('s');
Ws = 15/(s + 1.5e-2); #% Ws
Wt = Wm;              #% Wt
Weps = 5e-4;          #% Weps

plt.figure(3)
#bodemag(Ws,Wt,'--',w);
mag, phase, om  = bode(Ws, logspace(0,3), plot=False);
mag2,phase2,om2 = bode(Wt, logspace(0,3), plot=False);
plt.semilogx(om,  20*np.log10(mag), label='$W_S$');
plt.semilogx(om2, 20*np.log10(mag2), '--', label='$W_T$');
#legend('Ws','Wt',4);
plt.legend()

#%% 一般化プラントの定義
#Pn = P.nominal;
#systemnames   = 'Pn Ws Wt Weps';
#inputvar      = '[w1; w2; u]';
#outputvar     = '[Ws; Wt; Pn+Weps]';
#input_to_Pn   = '[w1 - u]';
#input_to_Ws   = '[w1 - u]';
#input_to_Wt   = '[ u ]';
#input_to_Weps = '[ w2 ]';
#G = sysic;
num = [[Ws.num[0][0],    [0], (-Ws).num[0][0]], 
       [         [0],    [0],    Wt.num[0][0]],
       [Pn.num[0][0], [Weps], (-Pn).num[0][0]]]
den = [[Ws.den[0][0],    [1], (-Ws).den[0][0]], 
       [         [1],    [1],    Wt.den[0][0]],
       [Pn.den[0][0],    [1], (-Pn).den[0][0]]]
G_ = tf(num, den)
G = tf2ss(G_)

#%% H-inf制御器の計算（実行4.1）
#[K,clp,gamma_min,hinf_info] = hinfsyn(G,1,1,'display','on');
K, CL, gam, rcond = control.hinfsyn(G,1,1)
print( gam )

plt.figure(4)
mag1, phase1, om1 = bode( P_nominal, plot=False );
plt.semilogx( om1, 20*np.log10(mag1), '--', label='$P_{nominal}$' );
mag2, phase2, om2 = bode( K, plot=False );
plt.semilogx( om2, 20*np.log10(mag2), label='$K$' );
plt.ylim(-60, 60);
plt.xlim(1e0, 1e2);
plt.legend()